유니티의 Vector3 에는 Lerp, Slerp라는 함수가 있다.
두 함수 모두 선형보간을 해서 두 지점사이의 위치를 계산하는 함수지만 두 함수 사이에는 큰 차이가 있다.
그리고 이 차이를 이해하려면 우선 선형 보간과 구면 선형 보간의 차이를 이해해야 한다.
이 포스트의 주제이기도 한 선형 보간과 구면 선형 보간의 차이를 알아보자.
선형 보간 (Linear interpolate)

선형 보간은 매우 간단한 개념이다.
두 지점을 선형으로 연결해서 두 지점사이의 위치를 파악하는 방법이다.
유니티에서 사용할 때는
a와 b 지점 사이의 길이를 1로 두고, f값에 따라 그에 비례한 위치를 Vector3로 반환한다고 생각하면 된다.
구면 선형 보간 (Spherically interpolate)
구면 선형 보간은 두 지점 사이의 위치를 파악한다는 것은 같지만, 곡선으로 파악하기 때문에 선형 보간보다 조금 더 어렵다.
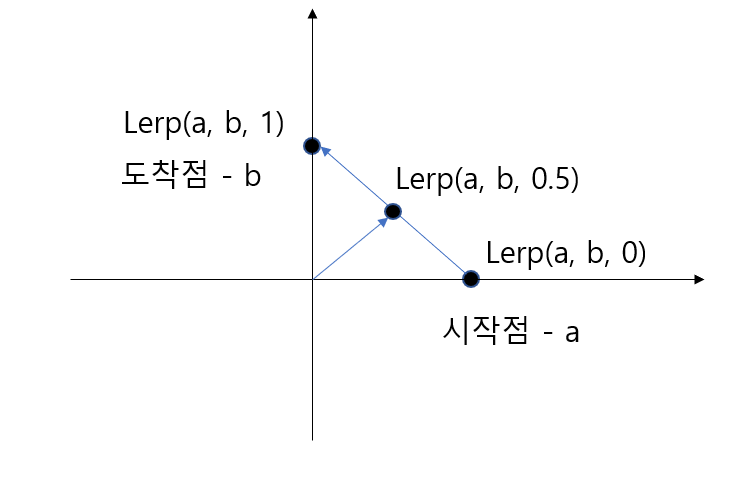
사실 아까 보았던 선형보간을 벡터로 설명하자면 이런 그림이다.
이러한 보간 방법은 평면 위에서는 정확하게 작동하지만, 만약 a와 b가 평평한 면이 아닌, 곡면 위의 점이라면 이야기가 달라진다.
우리의 키가 수천Km로 커지거나, 지구의 반경이 매우 작아져서 어린왕자의 별같이 변했다고 가정해보자.
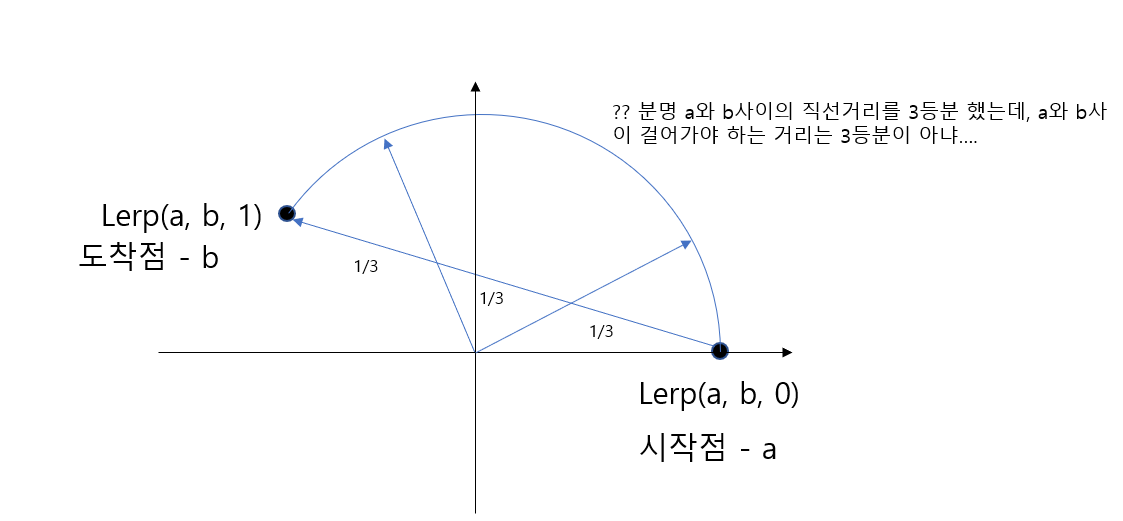
a는 서울이고, b는 런던이다. 우리는 서울부터 런던까지의 길이를 선형보간 해서 3등분을 하고, 걸어가기로 했다.
그렇다면 우리는 첫 날과 마지막 날은 쉬엄쉬엄 간다고 해도 두 번째 날 하루종일 걸어도 계획한 거리만큼 걸어갈 수 없을지도 모른다. 왜냐하면 우리는 곡면위에 있기 때문에 선형적인 보간으로는 실제 거리를 정확하게 나눌 수 없기 때문이다.
그래서 등장한 개념이 구면 선형 보간이다.
단순히 a와 b 두 점 사이의 거리를 나눠서 위치를 얻는 것이 아닌, a와 b가 구체평면 위에 위치한다고 가정한 후, 호의 거리를 선형적으로 보간해서 위치를 얻어내는 것이다.
그러므로 구면 선형 보간을 하는 경우, a와 b사이의 직선 거리를 보간하지 않고, a와 b사이에 포물선이 만들어진 후
그 포물선 위를 보간하는 것이다.
즉, 선형보간 = 평평한 면 위
구면 선형 보간 = 구면 위
라고 생각하면 된다.
마지막으로 레퍼런스를 확인해보자.
Lerp

두 지점 사이의 선형보간.
a와 b 사이의 선형보간을 t에 의해서 계산한 후 위치를 반환하며, 파라미터는 0~1의 값을 가지고 1은 endPoint, 0은 startPoint를 의미한다. ( 더 예를 들자면 t가 0.5라면 a와 b를 선형보간한 후 중앙 위치를 반환해 줄 것이다. )
즉 a를 0, b를 1로 생각해서 t에 비례한 a와 b사이의 위치를 Vector3형태로 반환해주는 것이다.
Slerp

두 지점 사이의 구면 선형 보간.
a와 b 사이의 구면 선형 보간을 t에 의해서 계산한 후 위치를 반환하며, 파라미터는 0~1의 값을 가지고 1은 endPoint, 0은 startPoint를 의미한다. ( 더 예를 들자면 t가 0.5라면 a와 b를 구면 선형 보간한 후 중앙 위치를 반환해 줄 것이다. )
즉 a를 0, b를 1로 생각해서 t에 비례한 a와 b사이의 위치를 Vector3형태로 반환해주는 것이다.
보다시피 두 함수의 차이는 Lerp는 선형 보간이고, Slerp는 구면 선형 보간이라는 것을 알 수 있다.
'ETC > Unity' 카테고리의 다른 글
| [유니티] 게임에서 Vector의 내적, 외적이 갖는 의의 (3) | 2020.02.29 |
|---|---|
| [유니티] 마우스 방향으로 2D Object 회전시키는 방법 (3) | 2020.02.29 |

