이 글은 RANSAC에 대해 아무것도 알지 못해도, 중학교 이상의 수학적 지식만 가지고 있다면 충분히 이해할 수 있도록 포스팅할 예정이다. 실제로 RANSAC은 매우 중요한 알고리즘이지만 실상 들여다보면 매우 간단한 구조이므로, 만약 이해하지 못한다면 그것은 독자의 문제가 아니라 쉬운 알고리즘을 쉽게 설명하지 못한 필자의 문제다.
RANSAC은 RANdom SAmple consensus의 약자로, 데이터셋에서 노이즈를 제거하고 모델을 예측하는 알고리즘이다.
매우 많은 분야에서 활용되며 특히 컴퓨터 비전 분야에서 광범위하게 사용된다.
RANSAC은 특정 임계값 이상의 데이터를 완전히 무시해버리는 특성이 있어 outlier에 강건한 알고리즘인데, 아래 그림을 보면 노이즈가 매우 크지만, 노이즈를 반영하지 않고 최대 데이터가 일치하는 이상적인 모델을 추출해내는 것을 볼 수 있다.
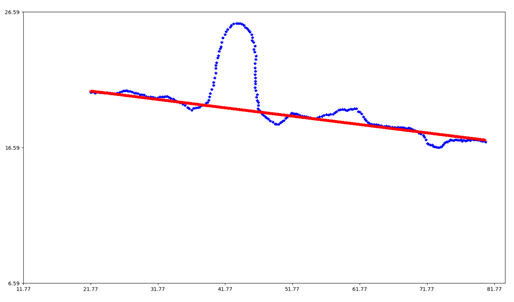
파란색은 노이즈가 섞인 데이터셋이고, 빨간색은 RANSAC을 통해 근사시킨 모델이다.
이제부터 RANSAC이 어떻게 모델을 생성하는지 알아보자.
RANSAC의 규칙

Hypothesis - 가설 단계
전체 데이터에서 N개의 샘플을 선택하고, 선택된 샘플을 통해 모델을 예측한다.
Verification - 검증단계
데이터셋에서 모델과 일치하는 데이터의 수를 센 후, 최대 값일 경우 모델 파라미터를 새롭게 저장한다.
RANSAC의 규칙은 매우 간단하다. 위 두 단계를 N번 반복하며, 그 중 최고의 모델을 출력해준다.
말로는 이해하기 힘들 수 있으니 그림으로 설명하겠다.

왼쪽 그림은 원본 데이터셋이다. 우리는 이 데이터셋이 직선형태를 지니며 노이즈가 첨가되어 있다는 것을 직관적으로 알 수 있다.
오른쪽에는 3개의 그림이 있는데, 각각 랜덤으로 데이터를 2개씩 추출한 후, 샘플(추출된 데이터)을 통해 모델을 예측한 그림이다. 초록색 실선은 모델이고, 실선의 위아래로 평행한 점선은 임계값을 첨가한 영역이다.
즉 우리는 초록색 실선을 모델로 삼고, 위아래 점선 내부에 있는 데이터들을 inlier라고 판단하는 것이다.
오른쪽 위 그림에서 뽑은 2개의 샘플로 1차함수 직선을 생성했을 때, 이 모델에 일치하는 데이터는 8개이다.
최초의 가설검증 단계이므로 이 모델은 우리의 결과 모델이 된다.
하지만 오른쪽 가운데 그림에서 다시 가설을 세운 결과, 새로운 모델에 일치하는 데이터는 10개이므로, 기존 최대값보다 크기 때문에 우리의 결과 모델은 해당 모델로 바뀌게 된다.
오른쪽 아래 그림에서도 다시 가설을 세우고 검증해보지만, 이번에는 3개의 데이터만이 모델에 일치하고, 기존 10개보다 일치하는 데이터가 적기 때문에 이 모델은 무시된다.
이제 슬슬 RANSAC의 기본 원리에 대해서 이해가 왔을 것이다.
위 과정을 계속 반복해서 조금씩 조금씩 좋은 모델을 찾고, N회 반복한 후 가장 좋은 모델을 출력해주는 것이 전부이다.
랜덤으로 데이터를 추출하는 과정에서는 수많은 경우에 수가 있다.
원하는 데이터들과 원하지 않는 데이터들이 무작위로 섞여 샘플로 사용될 것이다.
하지만, 이 과정을 무한히 반복하다보면 일정 확률로 우리가 원하는 데이터들만으로 이루어진 샘플이 추출될 것이고,
원하는 데이터들만 추출된다면 이상적인 샘플로 만들어진 이상적인 모델을 얻을 수 있을 것이다.
이 모델은 당연히 가장 많은 데이터와 일치할 것이고, 이 모델은 RANSAC알고리즘의 output이 되어 출력된다.
RANSAC의 파라미터
우리는 이상적인 데이터들만으로 샘플링 하고 싶지만, 데이터를 추출했을 때 현재 추출된 샘플이 모두 inlier인지 아닌지 판별할 수 없다. 그저 기존 값과 비교해서 일치하는 데이터가 더 많은가 적은가를 판단할 수 있을 뿐이다.
같은 이유로 RANSAC은 사용자가 종료 시점을 파악할 수 없는 알고리즘에 속한다. 기존보다 더 개선된 모델인지 아닌지만 판단할 수 있을 뿐 이것이 최고의 모델인지는 아무도 알 수 없는것이다.
하지만 우리는 유한시간 내에서 RANSAC알고리즘을 완료해야하기 때문에 종료 시점을 설정해주게 된다.
이 종료시점은 파라미터 N으로 불리며 RANSAC에서 T와 함께 가장 중요한 파라미터이다.

P = inlier로만 이루어진 샘플을 획득할 확률 – 샘플링 성공
α = dataset에서 inlier의 비율
m = 회당 추출하는 데이터 수
N = 알고리즘 반복 회수
RANSAC은 보통 p가 99.99% 이상으로 설정되어있다. 99.99% 확률로 최고의 모델을 출력해주는 반복횟수 N을 구한 뒤, 가설과 검증을 N회 거쳐서 그중 가장 좋은 모델을 출력하는 것이다.
파라미터 T는 threshold의 약자로 임계치의 의미이다. 모델을 예측하고, 데이터가 이 모델에 일치하는지 아닌지 판별할 때 모델과 데이터의 차이가 T보다 작으면 inlier, 크면 outlier로 구분하게된다.
간단하게 설명하자면 위에서 규칙을 설명할 때 점선과 실선 사이의 거리라고 생각하면 된다.
이 T는 대략적으로 수치를 정할 수 있는 N과 다르게 매우 민감한 파라미터이다.
일반적인 방법으로는 inlier들의 residual 분산을 σ2이라 할때, T = 2σ ~ 3σ 정도로 설정한다.
특히 상황에 따라 어댑티브하게 T를 설정하는 주제는 현재 RANSAC에서도 핫한 연구주제이다.
RANSAC의 한계
위에서 정의한 RANSAC의 원리를 통해 RANSAC이 가진 한계에 대해서 생각해보자.
1. Non-determisitic algorithm
RANSAC은 랜덤으로 샘플링하기 때문에 항상 같은 결과를 보장하지는 않는다. 파라미터에 따라서 알고리즘을 실행할 때마다 다른 모델이 출력될 수도 있다.
2. 불확실성
RANSAC은 inlier만으로 샘플링될 확률p를 위해 N번 반복하는 알고리즘이다.
매 주 로또에 당첨되는 사람은 99.99%와는 비교도 안될 확률로 상금을 받아간다. 아무리 반복해도 최상의 모델을 뽑지 못 할 가능성이 조금은 존재하는 것이다.
3. 데이터가 밀집되어있는 경우 반응이 미흡함

위 사진은 몇몇 모델근사 알고리즘의 loss error 그래프인데, RANSAC의 경우는 에러가 임계값 이하일 때 loss가 0이다.
모델과 임계값 이하의 차이만 가지고 있다면, 이 차이는 전혀 알고리즘에 반영되지 않고 단순히 임계값 내의 데이터로 집계되는 것이다. 이러한 원리때문에 RANSAC은 데이터가 밀집되어 있을 때 좋지 못할 모델을 출력 할 가능성이 있다.
해당 문제를 해결하기 위해 만든 알고리즘이 MLESAC인데, 관심이 있으면 검색해보는 것도 좋을 것 같다.
4. outlier가 특정 모델을 이루고 있을 경우
RANSAC은 샘플링된 데이터를 통해 모델을 만들고, 해당 모델과 일치하는 데이터의 수로만 결과를 출력하기 때문에, outlier가 특정 구조를 이루고 있고, 이러한 outlier들이 샘플링되어 데이터를 집계하게 된다면 상당히 많은 outlier가 이 잘못된 모델에 일치할 것이다. 그럴 경우 RANSAC은 잘못된 결과를 출력 할 가능성이 있다.