Lacam은 PIBT 기반의 MAPF 알고리즘입니다.
널리 사용되는 2레벨 구조를 가지고있지만,
모든 경우를 탐색하며 최적의 경로를 찾는 다른 MAPF와는 다르게 유망한 분기에 대해서만 탐색을 확장하는 독특한 방법으로 최적성의 정점을 찍은 MAPF입니다.
이전 논문인 PIBT와 유사하게 대규모 로봇의 실시간 경로생성을 위해 최적성과 연산량을 교환한 MAPF이며,
가성비가 상당히 좋아서 훌륭하다는 평가를 받는 MAPF중 하나입니다.
Lacam의 동작 원리
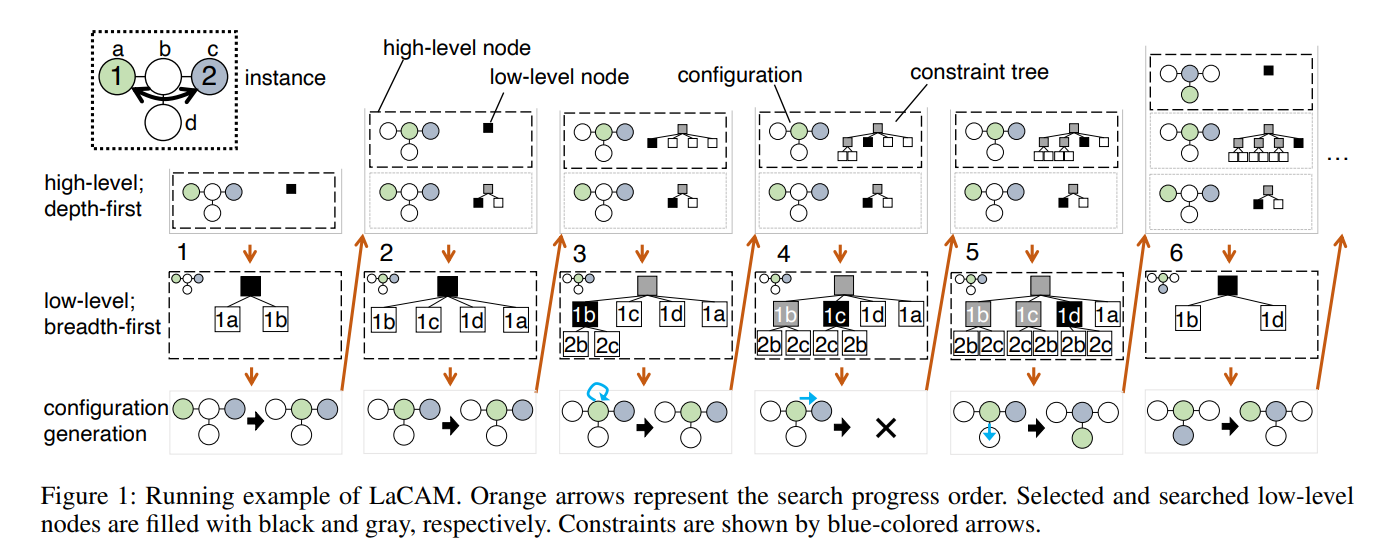
Lacam은 2레벨 구조를 가지고있습니다.
High-level은 Configuration을 넓이우선방식으로 탐색합니다. 여기서 Configuration은 특정 시간대의 모든 로봇 위치를 뜻합니다.
low-level은 High-level에서 가장 위에 있는 Configuration을 하나 가져와서 한 로봇에 대해 갈수있는 모든 인접노드를 Constraint tree에 추가한 후, 깊이우선방식으로 탐색합니다.
그리고 두 레벨에서 configuration과 한 로봇의 이동이 선택되면, configuration generation단계에서 해당 선택을 반영한 PIBT를 수행합니다. 그리고 PIBT의 결과가 PIBT수행전과 같다면 넘어가고, 다르다면 High-level의 맨 위에 PIBT의 결과를 Configuration으로 추가합니다.
Configuration이 Goal과 같아질때까지 위 절차를 계속 반복합니다.
위에서 디테일한 부분을 조금더 적자면..
low-level에서 Constraint tree의 깊이는 로봇의 수보다 깊어질 수 없습니다. 하나의 뎁스에서 하나의 로봇의 이동만 다루기 때문이죠.
그리고 low-level에서 어떤 로봇을 움직일지 선택하는건 사실 무작위로 해도 됩니다. 하나의 뎁스에서 하나의 로봇만 다루는 기본 조건만 있으면 중복없이 모든 로봇에 대해 탐색 가능하니까요. 본 논문의 저자는 최초 순서의 경우는 로봇과 도착지의 거리순으로, 이후에는 노드에 도착하지 않은 로봇들을 우선으로 처리했다고 합니다.
그리고 low-level에서 로봇을 어떤 방향으로 움직일지 constraint tree를 만드는 순서는 의외로 무작위로 넣었다고 하네요. 직관적으로 생각하면 골까지의 거리를 기반으로 넣으면 더 품질이 좋아지지 않을까 싶었는데 생각해보니 거리를 계산해서 비교하는것도 연산량을 무시할 수준이 아닐것같네요.
Lacam 성능 분석
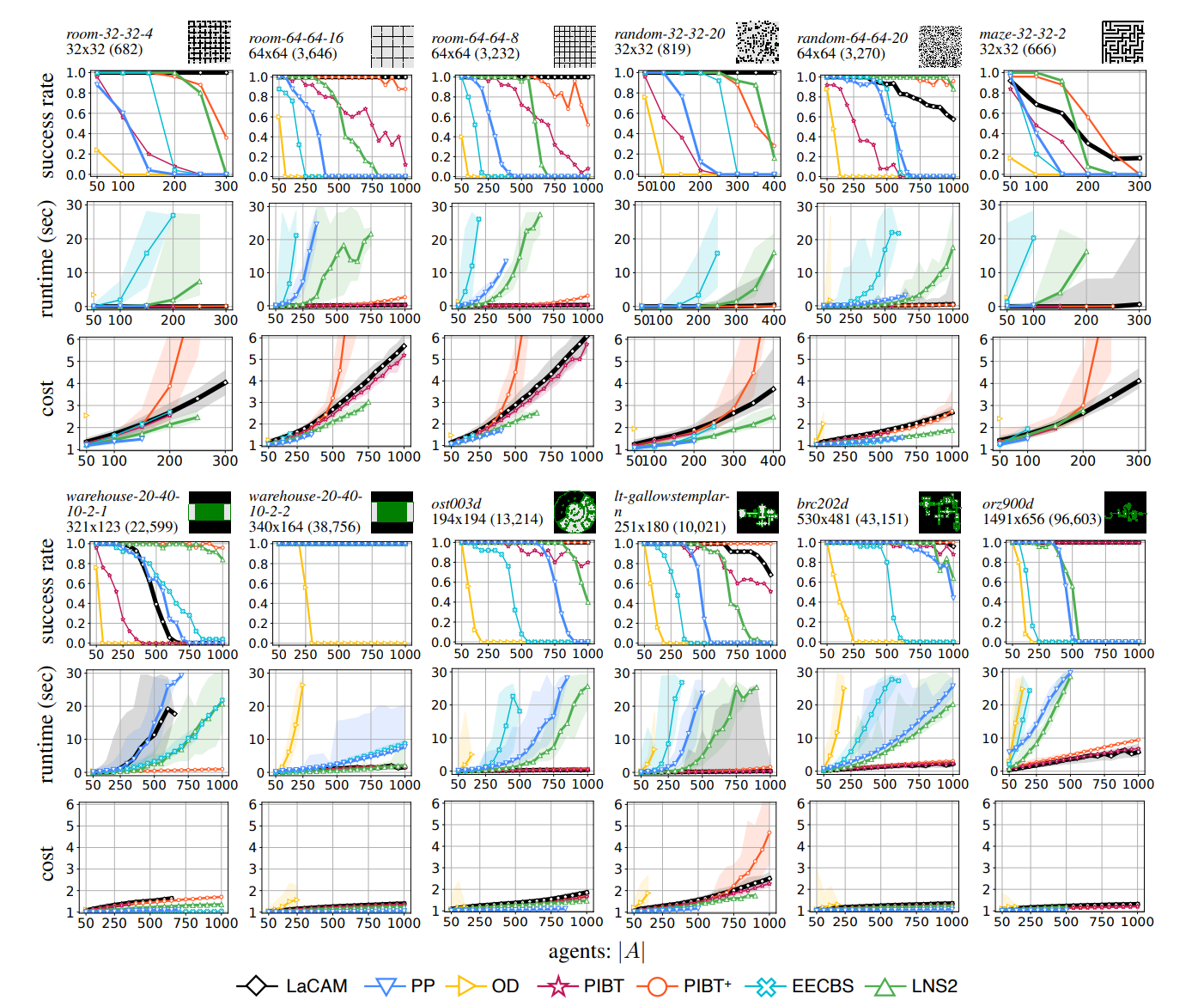
다양한 MAPF알고리즘과 비교를 했는데요, 결과가 상당히 재밌습니다.
Success Rate
우선 로봇이 많아질수록 다른 알고리즘들과 Success rate가 확연히 차이나는 이유는 시간때문이겠지요.
그만큼 최적성 확보에 기반한 타 알고리즘들이 대규모 관제 상황에서 얼마나 대응불가능한지 나타내는 부분이라고 할수 있습니다.
물론 로봇이 300대 이상 사용되는 현장은 거의 없다시피 하지만요.
Runtime
다른 알고리즘들과 비교가 민망할정도의 성능
Cost
코스트는 LNS를 따라갈수가 없습니다. 최적성을 포기하고 연산량을 감소시켰으니 어느정도 당연한 결과라고 생각합니다.
LNS도 정말 유명한 MAPF라 조만간 다뤄보고싶네요.
Adversarial Instance
정말 재미있는 부분은 왼쪽 아래의 warehouse 데이터셋인데요.
위 케이스들과는 다르게 다른 알고리즘들보다 시간이며 성공율이며 약세입니다.
이건 사실 Lacam의 구조적 한계가 아닌 PIBT의 한계입니다. Lacam은 다른 알고리즘들과는 다르게 PIBT알고리즘을 써서 로봇의 다음 액션을 정하는데요, PIBT논문을 보시면 아시겠지만 PIBT 자체가 좁은 통로의 해결을 힘들어합니다.
왜냐면 PIBT는 모든 로봇에 대해서 충돌과 코스트를 비교해가며 반드시 해결되는 결과를 출력하는게 아니라,
각 스텝마다 휴리스틱에 의해 선출된 우선순위에 따라 높은 우선순위 로봇의 코스트를 낮추는것을 기반으로 하기때문에
로봇들의 우선순위가 엎치락 뒷치락 하는 결과가 자주 나옵니다...
저자는 후속논문에서 Lacam을 개선한 Lacam2를 제안했는데, 이 문제를 해결하는게 논문의 핵심 내용중 하나더라고요 ㅋㅋ
Lacam은 현재 3까지 버젼이 있는데, 하나하나 문제를 해결하며 발전하는 모습이 멋있습니다.
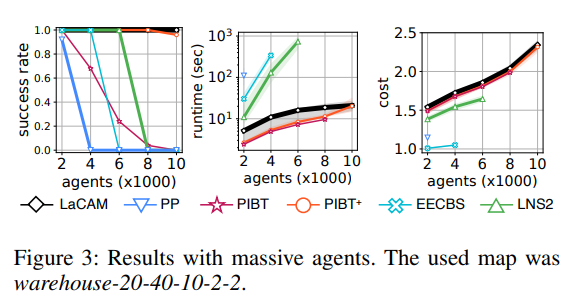
확장성 테스트입니다. warehouse지도에서 10,000대의 로봇을 사용해서 경로를 생성했습니다.
10,000대 규모의 로봇 경로계산에 30초정도 소모되었다고 하는데 대단한 속도인것은 분명하네요.
Lacam 성능의 비결
그러면 Lacam은 왜 이렇게 빠를까요?
이건 Lacam의 제한된 제약추가시스템 때문입니다.
기존 알고리즘들은 한번의 탐색마다 엄청난 개수의 분기를 생성합니다.
"모든 로봇의 위치가 정해졌을때, 다음 스텝에서 로봇들을 어떻게 움직일까"
는 <<로봇 숫자 * 각 로봇의 이웃숫자>>만큼의 조합 개수를 가집니다.
경우의 수가 엄청많죠. 그래서 이 모든 조합에 대해서 탐색하고 판단해야합니다.
하지만 Lacam의 경우는 어떤가요?
low-level에서 넓이우선으로 탐색하는 과정은 같았지만, 넓이우선 탐색 과정을 항상 끝냈나요?
아닙니다. PIBT를 활용하여 Configuration을 만들고, 해당 Configuration이 이전과 다른경우
새로운 configuration에 대해서 다시 넓이우선 탐색을 했죠.
PIBT는 높은 우선순위의 로봇의 코스트가 반드시 줄어들게 되어있습니다. 즉, Configuration이 제작되었다는 것은 거의 대부분의 상황에서 이전 Configuration보다 코스트가 줄었다는 것인데 이렇게 코스트가 감소한 경우에는 기존의 넓이우선탐색하던 Configuration을 버리고, 좀 더 유망한 Configuration에 대해서 탐색을 하다가, 실패한경우에 다시 Stack 아래에 있던 기존 configuration을 사용하게되죠.
이런 과정을 통해서 Lacam은 분기수를 극적으로 감소시켰고, 이것이 연산량 감소의 핵심 원인입니다.
마치며
PIBT부터 느꼈지만 참신하면서 성능까지 훌륭한 알고리즘들을 많이 생각해내시는것같습니다.
멋있다멋있어.



